RSA算法原理

本文借鉴了https://en.wikipedia.org/wiki/RSA_(cryptosystem) 中的资料和些图片

一、RSA加密过程：

（1）RSA基本原则：

​ RSA 背后的一个基本原则是观察到找到三个非常大的正整数 e、d 和 n 是可行的，使得对所有整数 m（0 ≤ m < n）进行模幂运算：

​ {\displaystyle (m^{e})^{d}\equiv m{\pmod {n}}}

​ 三杠表示模同余，也就是当调换e和d的位置，会有相同的余数

{\displaystyle (m^{d})^{e}\equiv m{\pmod {n}}.}

RSA 涉及公钥和私钥。公钥是众所周知的，用于加密消息。目的是使用公钥加密的消息只能在合理的时间内使用私钥解密。公钥由整数n和e表示，私钥由整数d表示（尽管在解密过程中也会使用n，因此它也可能被认为是私钥的一部分）。m代表消息。

（2）密钥生成：

RSA算法的密钥以下方式生成：

1.选择两个相差大的大质数 p 和 q

​ 为了使得因式分解更难，p和q要随机选择：为了选择它们，标准方法是选择随机整数并使用素数测试，直到找到两个素数。p和q应保密

2.计算n

​ n = p*q

​ n作为公钥和私钥的模数。它的长度，通常用比特来表示，就是密钥长度

3.计算λ ( n )

在数论这一数学分支中，正整数n的Carmichael 函数 λ ( n )是满足以下条件的 最小正整数m

a^{m}\equiv 1{\pmod {n}}

​ 在代数术语中，λ ( n )是整数乘法群对n取模的指数。

由于n = pq , λ ( n ) = lcm ( λ ( p ), λ ( q ))，并且由于p和q是素数，因此λ ( p ) = φ ( p ) = p − 1，同样地λ ( q ) = q − 1。因此λ( n ) = lcm( p − 1, q − 1)。

4.选择一个整数e使得2 < e < λ ( n )和gcd ( e , λ ( n )) = 1；也就是说，e和λ ( n )互质。

​ 最常选择的e值是2^16 + 1 =65537

​ e作为公钥的一部分发布

5.确定d

​ d ≡ e −1 (mod λ ( n ))；也就是说，d是e模λ ( n )的模乘逆

​

二、RSA解密过程：

​ 通过计算使得私钥指数从d到c恢复m

{\displaystyle c^{d}\equiv (m^{e})^{d}\equiv m{\pmod {n}}.}

示例：

image-20230507160332592

​ 但实际使用中国余数定理来加速因子模数的计算（mod pq 使用 mod p 和 mod q)

中国余数算法：

{\displaystyle d_{P}=d{\pmod {p-1}},}

​ {\displaystyle d_{Q}=d{\pmod {q-1}},}

​ {\displaystyle q_{\text{inv}}=q^{-1}{\pmod {p}}。}

image-20230507161311720

签名消息

假设 Alice 希望向 Bob 发送一条签名消息。她可以使用自己的私钥来这样做。她生成消息的散列值，将其计算为d的幂（模n）（就像她在解密消息时所做的那样），并将其作为“签名”附加到消息中。当 Bob 收到签名消息时，他使用相同的哈希算法结合 Alice 的公钥。他对签名求e次方（模n）（就像他在加密消息时所做的那样），并将生成的散列值与消息的散列值进行比较。如果两者一致，他就知道消息的作者拥有爱丽丝的私钥，并且消息自发送以来没有被篡改过。

这是运用了求幂规则：

image-20230507161804764

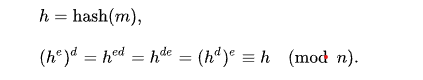
费马小定理

​ 如果p是素数，则对于任意的a，数a^p-a是p的整数倍。

​ a^p \equiv a \pmod p。

例如 a =2, p =7 则 2^7 = 128,128-2=126=7*18 为7的整数倍

如果a 不能被p整除，即如果a与p互质，费马小定理等价于（p^-1）-1是p的整数倍

a^{p-1} \equiv 1 \pmod p。

总结：

在RSA密码应用中，公钥是被公开的，即e和n的数值是可以被得到的。破解RSA密码就是从已知的额和n求得d。这样就可以使用私钥来破解密文了。

但当p和q是一个很大的素数时，从n去分解因子p和q，是数学界公认的难题。

因此，在进行RSA加密的时候，应尽量的使用足够大的p和q，来保证d不会被算出

但是，RSA的缺点也很明显：

​ RSA的安全性完全来自于因子分解，破译RSA的难度等价于分解因子的难度

​ 密钥的产生十分麻烦，受到p和q的影响，很难做到一次一个密钥

​ RSA需要更长的密钥，这就使得运算速度较慢。

最后修改：2023 年 08 月 20 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏